Division Algebras Dimensions
They have dimensions k 1 2 4 and 8. Stack Exchange network consists of 176 QA communities including Stack Overflow the largest most trusted online community for developers to learn share their knowledge and build their careers.
I The classical super-2-brane makes sense only in.

Division algebras dimensions. If we look at the field of real numbers Frobenius theorem states that the only finite dimensional associative division algebras over up to isomorphism are. ΨΨΨΨ0Psi cdot Psi cdot Psi Psi 0 holds in spacetimes of dimensions three higherthan those of the division algebras. Namely in these algebras the associator a b c a b c a b c abc a bc - ab c is completely antisymmetric.
3 Families hep-th9902016 19-spacetime to 13-spacetime. That is dimensions 4 5 7 and 11. Reduction to U1xSU2xSU3 hep-th9902050 Algebraic Spinor Reduction Yields the Standard Symmetry and Family Structure.
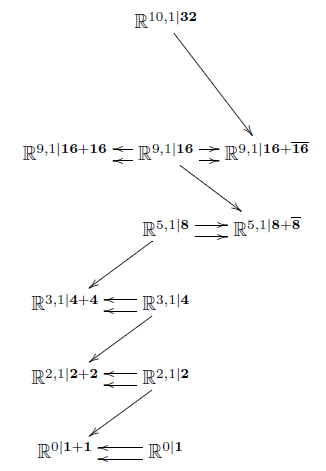
Starting from the four normed division algebras---the real numbers complex numbers quaternions and octonions with dimensions k 1 2 4 and 8 respectively---a systematic procedure gives a 3-cocycle on the Poincare Lie superalgebra in dimensions k 2 3 4 6 and 10. I The classical superstring also makes sense only in dimensions 3 4 6 and 10. The dimensions 2 8 and 24 play significant roles in lattice theory.
These division algebras can be. I The only YangMills theories with minimal supersymmetry occur in dimensions 3 4 6 and 10. The next step are the Sedenions S which are no longer a division algebra but still power-associative.
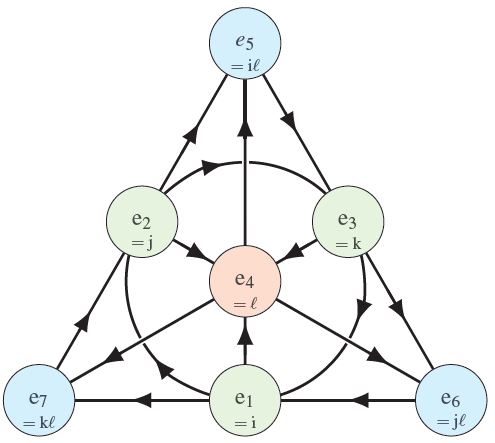
I The only normed division algebras are R C H and O. Bab 1 2 Na b Na Nb. For a unital composition algebra Awith quadratic form N we define a bilinearformbbythepolarizationformulafromthequadraticform.
3 4 6 and 10. The connection is visible from the fact that the normed division algebras have dimensions 1 2 4 and 8 while classical superstring theories and minimal super-YangMills theories live in spacetimes of dimension two higher. Supersymmetry and Division Algebras Introduction I The only normed division algebras are R C H and O.
We can go on forever doubling in each step the dimension of the algebra. The simplest classical super-2-brane theories make sense in spacetimes of dimensions three higher. We can use the division algebras to describe spinors and vectors in these magic dimensions.
A special feature of the normed division algebras make the identity true. A celebrated theorem of Milnor and Kervaire asserts that any finite dimensional not necessarily associative unital division algebra over the real numbers has dimension 124 or 8. I The classical superstring makes sense only in dimensions k 2 3 4 6 and 10.
4 5 7 and 11. The link of the Division Algebras to 10-dimensional spacetime and one leptoquark family is extended to 26-dimensional spacetime and three leptoquark families. Lie n-algebras supersymmetry and division algebras Introduction This research began as a puzzle.
They have dimensions 1 2 4 and 8. There are division algebras with centre Q of dimension n 2 for any positive integer n. 3 4 6 and 10.
The connection is visible from the fact that the normed division algebras have dimensions 1 2 4 and 8 while classical superstring theories and minimal super-YangMills theories live in spacetimes of dimension two higher. And this rule is why there exist supersymmetric 2-branes in these dimensions. The next step is no longer a division algebra the sedenions of dimension 16.
For n 3 they do not embed in H. These are all related. In Clifford algebra theory there are well-known periodicities of the first two of these dimensions.
This result is established using methods from algebraic topology such as K-Theory. The link of the Division Algebras to 10-dimensional spacetime and one leptoquark family is extended to 26-dimensional spacetime and three leptoquark families. Now on home page ads.

Division Algebra From Wolfram Mathworld
Geometry Of Physics Supersymmetry In Nlab
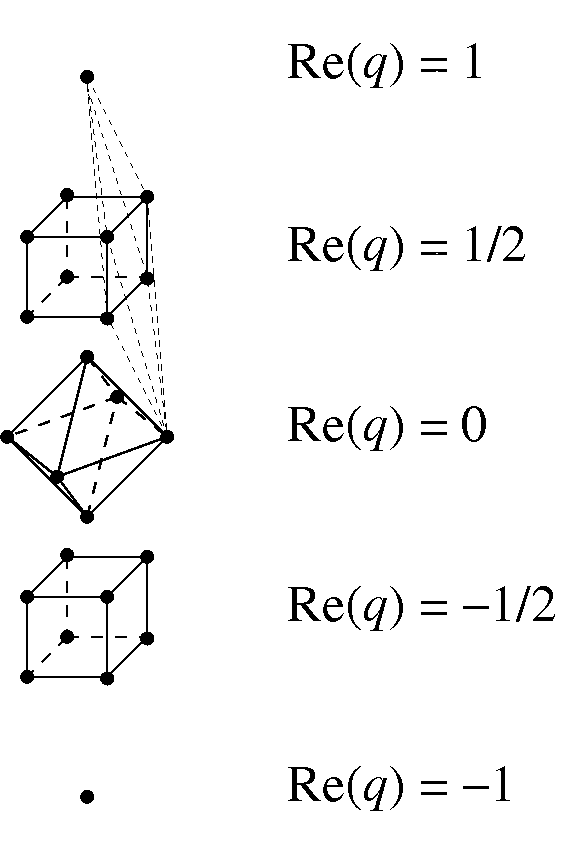
On Quaternions And Octonions By John Conway And Derek Smith

Division Algebra An Overview Sciencedirect Topics

Algebraically Closed Field In A Division Ring Mathematics Stack Exchange

Konrad Voelkel Classification Of Division Algebras

Proof Of Wedderburn S Theorem Mathematics Stack Exchange

Braids Normed Division Algebras And Standard Model Symmetries Sciencedirect

Finite Dimensional Division Algebras Over Fields Nathan Jacobson Springer

Ask Ethan Could Octonions Unlock How Reality Really Works

Dividing Polynomials College Algebra

Algebra Paper Retracted Because Of Questions About The Integrity Of The Mathematics Retraction Watch

Finite Dimensional Division Algebras Over Fields Nathan Jacobson Springer

Polynomial Long Division In Algebra 2 Polynomials College Algebra Teaching Algebra

Division Algebras And Physics Video 1 14 First Video General Audience Youtube
Normed Division Algebra In Nlab

Braids Normed Division Algebras And Standard Model Symmetries Sciencedirect

Pdf The Classification Of Real Division Algebras